伝搬損失
奥村-秦モデルをはじめ、各種電波伝搬モデルの “伝搬損失” を計算できます。
また、送信電力、送信アンテナ利得、受信アンテナ利得を入力すると、”電界強度”、”受信電力”を計算できます。
(一部の伝搬モデルを除く)
-
モデル選択
マクロセル(基地局アンテナを周囲の建物高よりも十分高い場所に設置)奥村-秦モデルマイクロセル(基地局アンテナを周囲の建物高と同程度の高い場所に設置)坂上モデルWalfisch-池上モデルストリートマイクロセル(基地局アンテナを周囲の建物高よりも十分低い場所に設置)平面大地伝搬モデル加地モデル市坪モデル-
モデル選択 :
市街地(大都市)市街地(中小都市)郊外地開放地周波数 \(f \ [{\rm MHz}]\)\([{\rm MHz}]\)150~2000の値を入力基地局アンテナ高 \(h_{\rm b} \ [{\rm m}]\)\([{\rm m}]\)30~200の値を入力移動局アンテナ高 \(h_{\rm m} \ [{\rm m}]\)\([{\rm m}]\)1~10の値を入力距離 \(d \ [{\rm km}]\)\([{\rm km}]\)1~20の値を入力-
送信電力 \(P_{\rm t} \ [{\rm W}]\)\([{\rm W}]\)数値を入力してください送信アンテナ利得 \(G_{\rm t} \ [{\rm dBi}]\)\([{\rm dBi}]\)数値を入力してください
-
受信アンテナ利得 \(G_{\rm r} \ [{\rm dBi}]\)\([{\rm dBi}]\)数値を入力してください
-
伝搬損失\(L_{\rm p}\)= XXX.XX \([{\rm dB}]\)
-
電界強度
-
受信電力
横軸 :周波数距離基地局高移動局高- 計算式 - 伝搬損失 (マクロセルモデル)
-
奥村―秦モデル
[周波数 : 150~1500MHz]\begin{align*} L_{p} = 69.55 + 26.16\log f - 13.82\log h_{\rm b} - a\left(h_{\rm m} \right) \qquad & \\ + \left(44.9 - 6.55\log h_{\rm b} \right)\log d + C & \end{align*} 市街地 大都市 \begin{align*} & C = 0 \\ & a\left(h_{\rm m}\right) = 8.29\{\log\left(1.54 h_{\rm m} \right)\}^{2} - 1.1 & \left(f \leq 400{\rm MHz}\right)\\ & a\left(h_{\rm m}\right) = 3.2\{\log\left(11.75 h_{\rm m} \right)\}^{2} - 4.97 & \left(f \geq 400{\rm MHz}\right) \end{align*} 中小都市 \begin{align*} & C = 0 \\ & a\left(h_{\rm m}\right) = \left(1.1\log f - 0.7 \right)h_{\rm m} - \left(1.56\log f -0.8 \right) \qquad \quad \end{align*} 郊外地 \begin{align*} & C = -2\{\log \left(f/28 \right)\}^{2} - 5.4 \\ & a\left(h_{\rm m}\right) = \left(1.1\log f - 0.7 \right)h_{\rm m} - \left(1.56\log f -0.8 \right) \qquad \quad \end{align*} 開放地 \begin{align*} & C = -4.78\left(\log f \right)^{2} + 18.33\log f - 40.94 \\ & a\left(h_{\rm m}\right) = \left(1.1\log f - 0.7 \right)h_{\rm m} - \left(1.56\log f -0.8 \right) \qquad \quad \end{align*} COST―Hata モデル
[周波数 : 1500~2000MHz]\begin{align*} L_{p} = 46.3 + 33.9\log f - 13.82\log h_{\rm b} - a\left(h_{\rm m} \right) \qquad & \\ + \left(44.9 - 6.55\log h_{\rm b} \right)\log d + C_{\rm M} & \end{align*} 市街地 大都市 \begin{align*} & C_{\rm M} = 3 \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad \end{align*} 中小都市 \begin{align*} & C_{\rm M} = 0 \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad \end{align*} -
パラメータ \(\ f\) 周波数 \([{\rm MHz}]\) \(\ 150 \sim 2000 {\rm MHz} \) \(\ h_{\rm b}\) 基地局アンテナ高 \([{\rm m}]\) \(\ 30 \sim 200 {\rm m} \) \(\ h_{\rm m}\) 移動局アンテナ高 \([{\rm m}]\) \(\ 1 \sim 10 {\rm m} \) \(\ d\) 距離 \([{\rm km}]\) \(\ 1 \sim 20 {\rm km} \) \(\ a\left(h_{\rm m}\right) \) 移動局アンテナ高に対する補正項 \(\ C_{\rm M} \) 都市の規模に応じた補正値 - 建物占有率 \(\alpha \)
- 建物を地面に投影した時の投影面積総和の全面積に対する割合 (500m×500m 区間)
-
\(\alpha \) 市街地 \(10 \% \sim \ \ \) 郊外地 \(2 \sim 10 \% \) 開放地 \(\sim 2\% \ \ \ \ \) 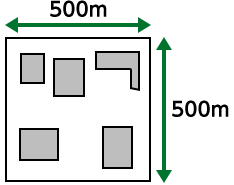
- 参考文献
- [1] 細矢良雄監修, "電波伝搬ハンドブック", リアライズ理工センター出版
- [2] 岩井誠人著, "移動通信における電波伝搬 ―無線通信シミュレーションのための基礎知識―", コロナ社
- [3] 奥村善久, 進士昌明監修, "移動通信の基礎", 社団法人電気情報通信学会
-
-
 周波数 \(f \ [{\rm MHz}]\)\([{\rm MHz}]\)450~2200の値を入力基地局アンテナ地上高 \(h_{\rm b0} \ [{\rm m}]\)
周波数 \(f \ [{\rm MHz}]\)\([{\rm MHz}]\)450~2200の値を入力基地局アンテナ地上高 \(h_{\rm b0} \ [{\rm m}]\)
(基地局の地面からの高さ)\([{\rm m}]\)0より大きい値を入力基地局アンテナ高 \(h_{\rm b} \ [{\rm m}]\)
(移動局がある地面からの高さ)\([{\rm m}]\)20~100の値を入力距離 \(d \ [{\rm km}]\)\([{\rm km}]\)0.5~10の値を入力道路幅 \(W \ [{\rm m}]\)\([{\rm m}]\)5~50の値を入力道路角 \(\theta \ [{\rm deg}]\)\([{\rm deg}]\)0~90の値を入力道路際の建物高 \(h_{\rm s} \ [{\rm m}]\)\([{\rm m}]\)5~80の値を入力平均建物高 \(\langle H \rangle \ [{\rm m}]\)
(移動局基地局方向 範囲内約20%)\([{\rm m}]\)5~50の値を入力基地局近傍の建物高 \(H \ [{\rm m}]\)\([{\rm m}]\)\(H \leq h_{\rm b0}\) の値を入力-
送信電力 \(P_{\rm t} \ [{\rm W}]\)\([{\rm W}]\)数値を入力してください送信アンテナ利得 \(G_{\rm t} \ [{\rm dBi}]\)\([{\rm dBi}]\)数値を入力してください
-
受信アンテナ利得 \(G_{\rm r} \ [{\rm dBi}]\)\([{\rm dBi}]\)数値を入力してください
-
伝搬損失\(L \)= XXX.XX \([{\rm dB}]\)
-
電界強度
-
受信電力
横軸 :周波数距離- 計算式 - 伝搬損失 (坂上モデル)
-
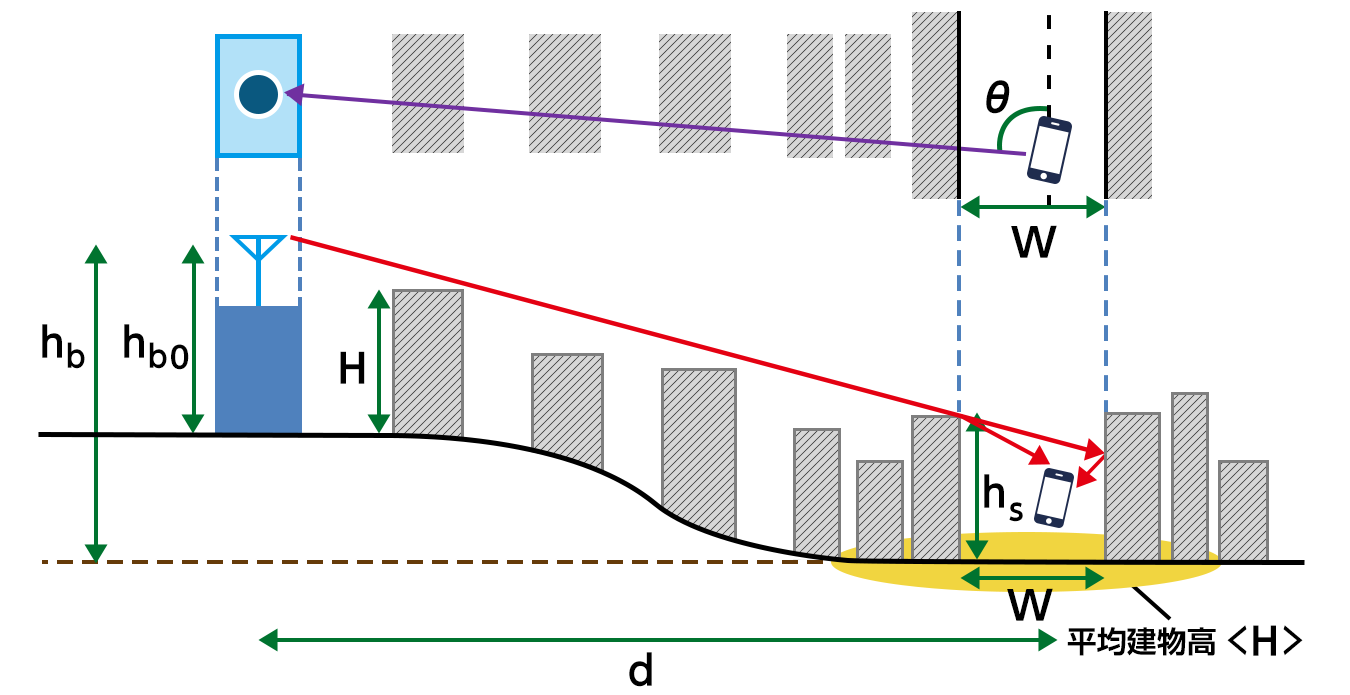
伝搬損失 \begin{align*} L = \ & 100 - 7.1\log W + 0.023\theta + 1.4\log h_{\rm s} + 6.11\log \langle H\rangle \\ & - \left\{24.37 - 3.7\left(\frac{H}{h_{\rm b0}} \right)^{2}\right\}\log h_{\rm b} + \left(43.42 - 3.1\log h_{\rm b} \right)\log d \\ & + 20\log f + {\rm exp}\left\{13\left(\log f - 3.23 \right) \right\} \end{align*} -
パラメータ \(\ f\) 周波数 \([{\rm MHz}]\) \(\ 450 \sim 2200 {\rm MHz}\) \(\ h_{\rm b0}\) 基地局アンテナ地上高 \([{\rm m}]\) (基地局の地面からの高さ) \(\ h_{\rm b0} > 0\) \(\ h_{\rm b}\) 基地局アンテナ高 \([{\rm m}]\) (移動局がある地面からの高さ) \(\ 20 \sim 100 {\rm m}\) \(\ d\) 距離 \([{\rm km}]\) \(\ 0.5 \sim 10 {\rm km}\) \(\ W \) 道路幅 \([{\rm m}]\) \(\ 5 \sim 50 {\rm m}\) \(\ \theta \) 道路角 \([{\rm deg}]\) \(\ 0 \sim 90 {\rm deg}\) \(\ h_{\rm s} \) 道路際の建物高 \([{\rm m}]\) \(\ 5 \sim 80 {\rm m}\) \(\langle H\rangle \) 平均建物高 \([{\rm m}]\) (移動局のある地面からの高さ)
[移動局から基地局方向の約20%の距離範囲内]\(\ 5 \sim 50 {\rm m}\) \(\ H \) 基地局近傍の建物高 \([{\rm m}]\) (基地局の地面からの高さ) \(\ H \leq h_{\rm b0}\)
*移動局アンテナ高は1.5mとする
- 参考文献
- [1] 細矢良雄監修, "電波伝搬ハンドブック", リアライズ理工センター出版
- [2] 岩井誠人著, "移動通信における電波伝搬 ―無線通信シミュレーションのための基礎知識―", コロナ社
- [3] 坂上修二, 久保井潔, "市街地構造を考慮した伝搬損の推定", 電子情報通信学会論文誌B, VolJ74-B-II, No.1, pp.17-25.
-
-
 モデル選択 :大都市中小都市周波数 \(f \ [{\rm MHz}]\)\([{\rm MHz}]\)800~2000の値を入力基地局アンテナ高 \(h_{\rm b} \ [{\rm m}]\)\([{\rm m}]\)4~50の値を入力移動局アンテナ高 \(h_{\rm m} \ [{\rm m}]\)\([{\rm m}]\)1~3の値を入力距離 \(d \ [{\rm km}]\)\([{\rm km}]\)0.02~5の値を入力道路幅 \(W \ [{\rm m}]\)\([{\rm m}]\)0より大きい値を入力道路角 \(\theta \ [{\rm deg}]\)\([{\rm deg}]\)0~90の値を入力建物高 \(h_{\rm roof} \ [{\rm m}]\)\([{\rm m}]\)\(h_{\rm m} < h_{\rm roof} < h_{\rm b} \) の値を入力建物間隔 \(b \ [{\rm m}]\)\([{\rm m}]\)0より大きい値を入力
モデル選択 :大都市中小都市周波数 \(f \ [{\rm MHz}]\)\([{\rm MHz}]\)800~2000の値を入力基地局アンテナ高 \(h_{\rm b} \ [{\rm m}]\)\([{\rm m}]\)4~50の値を入力移動局アンテナ高 \(h_{\rm m} \ [{\rm m}]\)\([{\rm m}]\)1~3の値を入力距離 \(d \ [{\rm km}]\)\([{\rm km}]\)0.02~5の値を入力道路幅 \(W \ [{\rm m}]\)\([{\rm m}]\)0より大きい値を入力道路角 \(\theta \ [{\rm deg}]\)\([{\rm deg}]\)0~90の値を入力建物高 \(h_{\rm roof} \ [{\rm m}]\)\([{\rm m}]\)\(h_{\rm m} < h_{\rm roof} < h_{\rm b} \) の値を入力建物間隔 \(b \ [{\rm m}]\)\([{\rm m}]\)0より大きい値を入力-
送信電力 \(P_{\rm t} \ [{\rm W}]\)\([{\rm W}]\)数値を入力してください送信アンテナ利得 \(G_{\rm t} \ [{\rm dBi}]\)\([{\rm dBi}]\)数値を入力してください
-
受信アンテナ利得 \(G_{\rm r} \ [{\rm dBi}]\)\([{\rm dBi}]\)数値を入力してください
-
伝搬損失\(L\)= XXX.XX \([{\rm dB}]\)
-
電界強度
-
受信電力
横軸 :周波数距離- 計算式 - 伝搬損失(Walfisch-池上モデル)
-
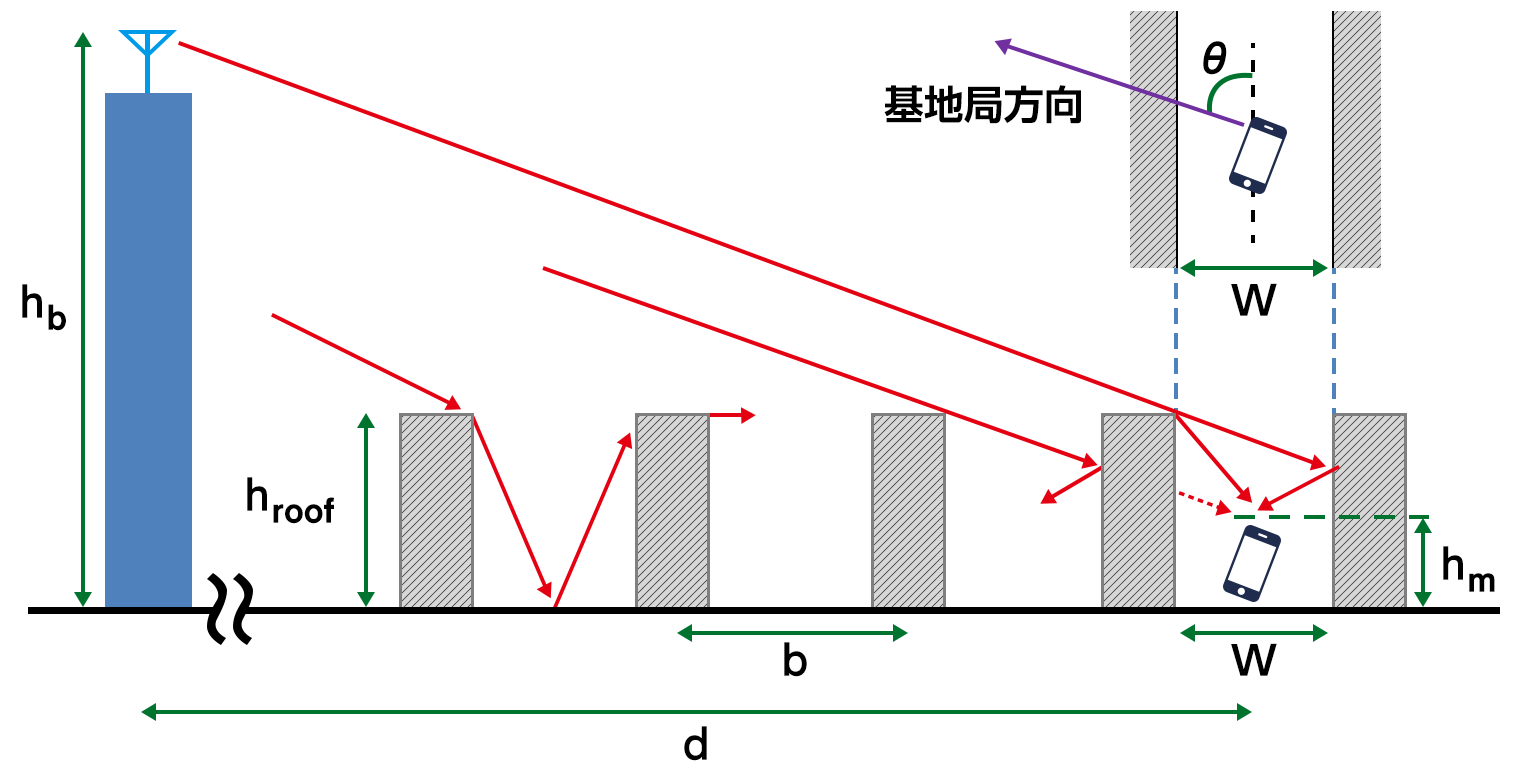
伝搬損失 \begin{align*} L = L_{0} + L_{\rm rts} + L_{\rm msd} \end{align*} 自由空間損失 \begin{align*} & L_{0} = 20 \log\left(\frac{4 \pi d}{\lambda} \right) = 32.4 + 20\log d + 20\log f \end{align*} 回折損失
[基地局と移動局間にある建物]\begin{align*} L_{\rm rts} = & -16.9 - 10\log W + 10\log f + 20\log\Delta h_{\rm m} \\ & + \left\{ \begin{array}{ll} -10 + 0.354\theta & \left(0 \leq \theta < 35^\circ \right) \\ 2.5 + 0.075\left(\theta-35\right) & \left(35 \leq \theta < 55^\circ\right) \\ 4.0 - 0.144\left(\theta-55\right) & \left(55 \leq \theta \leq 90^\circ\right) \end{array} \right. \\ \\ \Delta h_{\rm m} = & \ h_{\rm roof} - h_{\rm m} \ \ \left(h_{\rm roof} > h_{\rm m} \right) \end{align*} 回折/反射損失
[移動局近傍の建物と移動局間]\begin{align*} L_{\rm msd} = & \ 54 - 18\log\left(1 + \Delta h_{\rm b}\right) + 18\log d - 9\log b \\ & + \left\{ \begin{array}{ll} \left[-4 + 1.5\left(f/925 - 1\right)\right] & \left(\mbox{大都市} \right) \\ \left[-4 + 0.7\left(f/925 - 1\right)\right] & \left(\mbox{中小都市} \right) \end{array} \right. \\ \\ \Delta h_{\rm b} = & \ h_{\rm b} - h_{\rm roof} \ \ \left(h_{\rm b} > h_{\rm roof} \right) \end{align*} -
パラメータ \(\ f\) 周波数 \([{\rm MHz}]\) \(\ 800 \sim 2000 {\rm MHz}\) \(\ h_{\rm b}\) 基地局アンテナ高 \([{\rm m}]\) \(\ 4 \sim 50 {\rm m}\) \(\ h_{\rm m}\) 移動局アンテナ高 \([{\rm m}]\) \(\ 1 \sim 3 {\rm m}\) \(\ d\) 距離 \([{\rm km}]\) \(\ 0.02 \sim 5 {\rm km}\) \(\ W \) 道路幅 \([{\rm m}]\) \(\ W > 0\) \(\ \theta \) 道路角 \([{\rm deg}]\) \(\ 0 \sim 90 {\rm deg}\) \(\ h_{\rm roof} \) 建物高 \([{\rm m}]\) \(\ h_{\rm m} < h_{\rm roof} < h_{\rm b}\) \(\ b \) 建物間隔 \([{\rm m}]\) \(\ b > 0\) - 参考文献
- [1] 細矢良雄監修, "電波伝搬ハンドブック", リアライズ理工センター出版
- [2] 岩井誠人著, "移動通信における電波伝搬 ―無線通信シミュレーションのための基礎知識―", コロナ社
 周波数 \(f \ [{\rm MHz}]\)\([{\rm MHz}]\)0より大きい値を入力基地局アンテナ高 \(h_{\rm b} \ [{\rm m}]\)\([{\rm m}]\)数値を入力してください移動局アンテナ高 \(h_{\rm m} \ [{\rm m}]\)\([{\rm m}]\)数値を入力してください距離 \(d \ [{\rm km}]\)\([{\rm km}]\)0より大きい値を入力大地反射係数 (振幅) \(\gamma \)数値を入力してください大地反射係数 (位相) \(\phi \)
周波数 \(f \ [{\rm MHz}]\)\([{\rm MHz}]\)0より大きい値を入力基地局アンテナ高 \(h_{\rm b} \ [{\rm m}]\)\([{\rm m}]\)数値を入力してください移動局アンテナ高 \(h_{\rm m} \ [{\rm m}]\)\([{\rm m}]\)数値を入力してください距離 \(d \ [{\rm km}]\)\([{\rm km}]\)0より大きい値を入力大地反射係数 (振幅) \(\gamma \)数値を入力してください大地反射係数 (位相) \(\phi \)
[deg→rad 自動変換]\([{\rm deg}]\)数値を入力してください-
送信電力 \(P_{\rm t} \ [{\rm W}]\)\([{\rm W}]\)数値を入力してください送信アンテナ利得 \(G_{\rm t} \ [{\rm dBi}]\)\([{\rm dBi}]\)数値を入力してください
-
受信アンテナ利得 \(G_{\rm r} \ [{\rm dBi}]\)\([{\rm dBi}]\)数値を入力してください
-
伝搬損失\(L\)= XXX.XX \([{\rm dB}]\)
-
電界強度
-
受信電力
横軸 :周波数距離振幅位相* 入力した数値によって、第2項の真数が0に近い値を取る場合があります。- 計算式 - 伝搬損失(平面大地伝搬モデル)
-
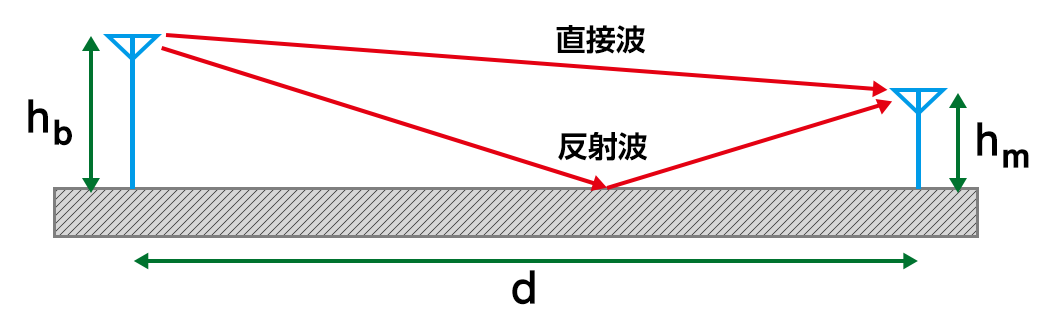
伝搬損失 \begin{align*} L &= 20\log\left(\frac{4\pi d}{\lambda} \right) - 10\log\left\{1 + \gamma^{2} + 2\gamma\cos\left(\frac{2 \pi \Delta l}{\lambda} + \phi \right) \right\} \\ \end{align*} 伝搬距離差 \begin{align*} \ \Delta l = \frac{2 h_{\rm b} h_{\rm m}}{d} \qquad \qquad \qquad \qquad \qquad \end{align*} 近似式 \(\lambda d < h_{\rm b},\ h_{\rm m} \) の領域 \begin{align*} L \fallingdotseq 20\log\left(\frac{4\pi d}{\lambda} \right) - 20\log\left(1+\gamma \right) \end{align*} \(d \gg h_{\rm b},\ h_{\rm m} \) の領域
(反射波が地面にほとんど水平入射)
[\(\gamma=1,\ \ \phi=\pi\)]\begin{align*} L \fallingdotseq 20\log\left(\frac{d^{2}}{h_{\rm b}h_{\rm m}} \right) \qquad \qquad \qquad \end{align*} -
パラメータ \(\ \lambda\) 波長 \([{\rm m}]\) \(\ h_{\rm b}\) 基地局アンテナ高 \([{\rm m}]\) \(\ h_{\rm m}\) 端末アンテナ高 \([{\rm m}]\) \(\ d\) 距離 \([{\rm m}]\) \(\ \Delta l \) 直接波と反射波の伝搬距離差 \([{\rm m}]\) \(\ \gamma \) 大地の反射係数(振幅) \([\gamma \exp\left(j \phi \right)]\) \(\ \phi \) 大地の反射係数(位相) \([\gamma \exp\left(j \phi \right)]\) - 参考文献
- [1] 細矢良雄監修, "電波伝搬ハンドブック", リアライズ理工センター出版
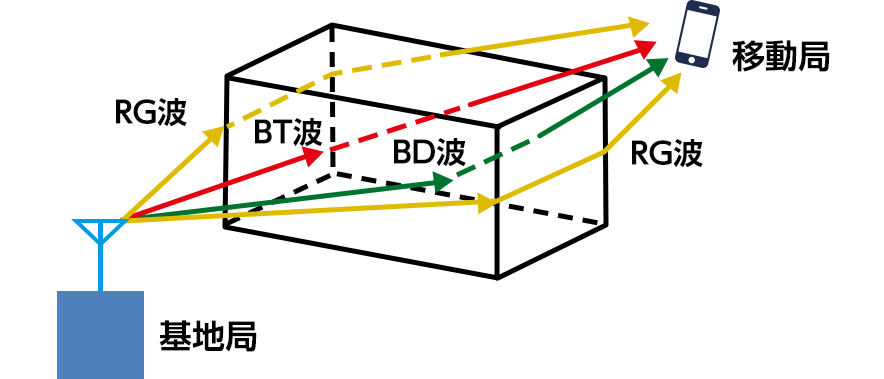 選択 :建物透過波 [BT波]道路伝搬波 [RG波]建物回折波 [BD波]
選択 :建物透過波 [BT波]道路伝搬波 [RG波]建物回折波 [BD波]-
自由空間損失 \(L_{\rm 10} \ [{\rm dB}]\)\([{\rm dB}]\)数値を入力してください減衰定数 \(a_{\rm 11} \ [{\rm dB/m}]\)\([{\rm dB/m}]\)数値を入力してください直線距離 \(d \ [{\rm m}]\)\([{\rm m}]\)数値を入力してください減衰量 \(b_{\rm 11} \ [{\rm dB/m}]\)
(コンクリート建物)\([{\rm dB/m}]\)数値を入力してください減衰量 \(b_{\rm 12} \ [{\rm dB/m}]\)
(木造建物)\([{\rm dB/m}]\)数値を入力してください減衰量 \(b_{\rm 13} \ [{\rm dB/m}]\)
(樹木)\([{\rm dB/m}]\)数値を入力してください透過距離 \(d_{\rm 11} \ [{\rm m}]\)
(コンクリート建物)\([{\rm m}]\)数値を入力してください透過距離 \(d_{\rm 12} \ [{\rm m}]\)
(木造建物)\([{\rm m}]\)数値を入力してください透過距離 \(d_{\rm 13} \ [{\rm m}]\)
(樹木)\([{\rm m}]\)数値を入力してください -
自由空間損失 \(L_{\rm 20} \ [{\rm dB}]\)\([{\rm dB}]\)数値を入力してください減衰定数 \(a_{\rm 21} \ [{\rm dB/m}]\)\([{\rm dB/m}]\)数値を入力してください道路長 \(l \ [{\rm m}]\)\([{\rm m}]\)数値を入力してください道路一曲がりの損失 \(b_{\rm 21} \ [{\rm dB}]\)\([{\rm dB}]\)数値を入力してください総曲がり回数 \(n \)数値を入力してください
-
自由空間損失 \(L_{\rm 30} \ [{\rm dB}]\)\([{\rm dB}]\)数値を入力してください減衰定数 \(a_{\rm 31} \ [{\rm dB/m}]\)\([{\rm dB/m}]\)数値を入力してください直線距離 \(d \ [{\rm m}]\)\([{\rm m}]\)数値を入力してください基地局側の回折損失 \(L _{\rm dt} \ [{\rm dB}]\)\([{\rm dB}]\)数値を入力してください移動局側の回折損失 \(L _{\rm dr} \ [{\rm dB}]\)\([{\rm dB}]\)数値を入力してください
伝搬損失\(L\)= XXX.XX \([{\rm dB}]\)- 計算式 - 伝搬損失(加地モデル)
-
伝搬損失 建物透過波 [BT波] \begin{align*} L_{1} = L_{10} + a_{11}d + b_{11}d_{11} + b_{12}d_{12} + b_{13}d_{13} \end{align*} 道路伝搬波 [RG波] \begin{align*} L_{2} = L_{20} + a_{21}l + b_{21}n \qquad \qquad \qquad \qquad \ \ \end{align*} 建物回折 [BD波] \begin{align*} L_{3} = L_{30} + a_{31}d + L_{\rm dt} + L_{\rm dr} \qquad \qquad \qquad \end{align*} -
パラメータ \(\ L_{10}, L_{20}, L_{30} \ \) 自由空間損失 \([{\rm dB}]\) \(\ a_{11}, a_{21}, a_{31} \ \) 減衰定数 \([{\rm dB/m}]\) \(\ b_{11}, b_{12}, b_{13} \ \) 単位長の減衰量 (コンクリート建物, 木造建物, 樹木) \([{\rm dB/m}]\) \(\ b_{21} \ \) 道路一曲りあたりの損失量 \([{\rm dB}]\) \(\ d \ \) 直線距離 \([{\rm m}]\) \(\ d_{11}, d_{12}, d_{13} \ \) 透過距離 \([{\rm m}]\) \(\ l \) 道路長 \([{\rm m}]\) \(\ n \) 総曲がり回数 \(\ L_{\rm dt} \) 基地局側の回折損失 \([{\rm dB}]\) \(\ L_{\rm dr} \) 移動局側の回折損失 \([{\rm dB}]\) - 参考文献
- [1] 細矢良雄監修, "電波伝搬ハンドブック", リアライズ理工センター出版
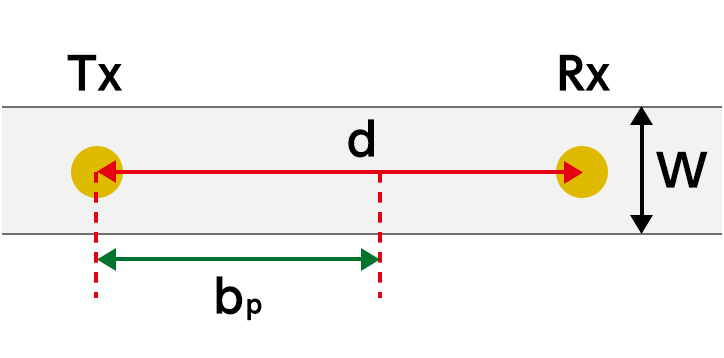
モデル選択 :見通し内道路交差道路平行道路周波数 :800MHz1400MHz基地局アンテナ高 \(h_{\rm b} \ [{\rm m}]\)\([{\rm m}]\)0より大きい値を入力移動局アンテナ高 \(h_{\rm m} \ [{\rm m}]\)\([{\rm m}]\)0より大きい値を入力-
距離 \(d \ [{\rm m}]\)\([{\rm m}]\)0より大きい値を入力道路幅 \(W \ [{\rm m}]\)\([{\rm m}]\)0より大きい値を入力
-
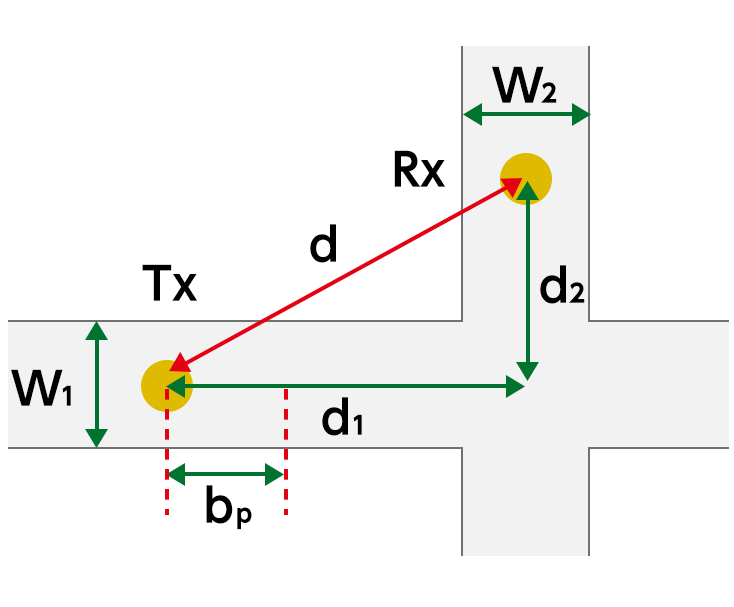
見通し道路上の距離 \(d_{1} \ [{\rm m}]\)
(基地局交差点間)\([{\rm m}]\)0より大きい値を入力交差道路上の距離 \(d_{2} \ [{\rm m}]\)
(交差点移動局間)\([{\rm m}]\)0より大きい値を入力道路幅 \(W_{1} \ [{\rm m}]\)\([{\rm m}]\)0より大きい値を入力道路幅 \(W_{2} \ [{\rm m}]\)\([{\rm m}]\)0より大きい値を入力 -
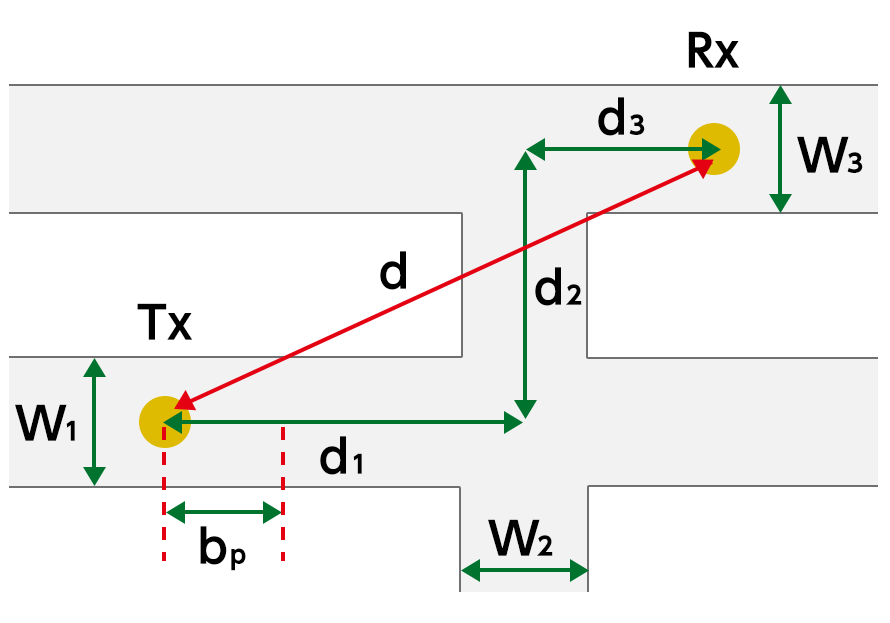
基地局から1番目の道路道 \(d_{1} \ [{\rm m}]\)\([{\rm m}]\)0より大きい値を入力基地局から2番目の道路道 \(d_{2} \ [{\rm m}]\)\([{\rm m}]\)0より大きい値を入力基地局から3番目の道路道 \(d_{3} \ [{\rm m}]\)\([{\rm m}]\)0より大きい値を入力道路幅 \(W_{1} \ [{\rm m}]\)\([{\rm m}]\)0より大きい値を入力道路幅 \(W_{2} \ [{\rm m}]\)\([{\rm m}]\)0より大きい値を入力道路幅 \(W_{3} \ [{\rm m}]\)\([{\rm m}]\)0より大きい値を入力
ブレークポイント距離 \(b_{\rm p} \ [{\rm m}]\)XXX.XX \([{\rm m}]\)-
送信電力 \(P_{\rm t} \ [{\rm W}]\)\([{\rm W}]\)数値を入力してください送信アンテナ利得 \(G_{\rm t} \ [{\rm dBi}]\)\([{\rm dBi}]\)数値を入力してください
-
受信アンテナ利得 \(G_{\rm r} \ [{\rm dBi}]\)\([{\rm dBi}]\)数値を入力してください
-
伝搬損失\(L\)= XXX.XX \([{\rm dB}]\)
-
電界強度
-
受信電力
- 計算式 - 伝搬損失(市坪モデル)
-
伝搬損失 見通し内道路 \begin{align*} & L = 20\log\ A + 43.3\log B - 15.5\log W + \left\{ \begin{array}{ll} 54.3 & \left(800 {\rm MHz}\right) \\ 59.9 & \left(1400 {\rm MHz}\right) \\ \end{array} \right. \\ & \ \ \left\{ \begin{array}{ll} A = d, & B = 1/b_{\rm p} & \left(d < b_{\rm p} \right) \\ A = b_{\rm p}, & B = d/b^{2}_{\rm p} & \left(d \geq b_{\rm p} \right) \end{array} \right. \end{align*} 交差道路 \begin{align*} & L = 20\log\ A + 39\log B - 20\log \left(W_{1} W_{2}\right) + \left\{ \begin{array}{ll} 68.5 & \left(800 {\rm MHz}\right) \\ 72.5 & \left(1400 {\rm MHz}\right) \\ \end{array} \right. \\ & \ \ \left\{ \begin{array}{ll} A = d_{1}d_{2}, & B = 1 & \left(d_{1}, \ d_{2} < b_{\rm p} \right) \\ A = b^{2}_{\rm p}, & B = d_{1}d_{2}/b^{2}_{\rm p} & \left(d_{1}, \ d_{2} \geq b_{\rm p} \right) \\ A = d_{1}d_{2}, & B = d_{1}d_{2}/b^{2}_{\rm p} & \left(\mbox{otherwise}\right) \end{array} \right. \end{align*} 平行道路 \begin{align*} & L = 20\log\ A + 22.5\log B + 40.4\log d_{2} + 18.6\log d^{'}_{3} \\ & - 15.4\log W_{1} - 19.9\log W_{2} -8.5\log W_{3} + \left\{ \begin{array}{ll} 35.6 & \left(800 {\rm MHz}\right) \\ 40.6 & \left(1400 {\rm MHz}\right) \\ \end{array} \right. \\ & \ \ \left\{ \begin{array}{ll} A = d_{1}, & B = 1/b_{\rm p} & \left(d_{1} < b_{\rm p} \right) \\ A = b_{\rm p}, & B = d_{1}/b_{\rm p} & \left(d_{1} \geq b_{\rm p} \right) \end{array} \right. \\ \\ & d^{''}_{3} = \frac{d_{2}+d_{3}}{d_{2}} \end{align*} ブレークポイント距離 \begin{align*} b_{\rm p} = \frac{2 \pi h_{\rm b} h_{\rm m}}{\lambda}\\ \end{align*} -
パラメータ \(\ h_{\rm b}\) 基地局アンテナ高 \([{\rm m}]\) \(\ h_{\rm m}\) 端末アンテナ高 \([{\rm m}]\) \(\ d\) 距離 \([{\rm m}]\) \(\ W\) 道路幅 \([{\rm m}]\) \(\ b_{\rm p}\) 基地局アンテナとブレークポイントの距離 \([{\rm m}]\) \(\ d_{1}\) <交差道路> 基地局から交差点までの見通し道路上の距離 \([{\rm m}]\)
<平行道路> 基地局から1番目の道路長 \([{\rm m}]\)\(\ d_{2}\) <交差道路> 交差点から移動局までの交差道路上の距離 \([{\rm m}]\)
<平行道路> 基地局から2番目の道路長 \([{\rm m}]\)\(\ d_{3}\) <平行道路> 基地局から3番目の道路長 \([{\rm m}]\) \(\ W_{1}, W_{2}, W_{3} \ \) <平行道路> 道路幅 \([{\rm m}]\) - 参考文献
- [1] 細矢良雄監修, "電波伝搬ハンドブック", リアライズ理工センター出版
- [2] 岩井誠人著, "移動通信における電波伝搬 ―無線通信シミュレーションのための基礎知識―", コロナ社
- [3] 市坪信一, 今井哲朗, "低アンテナ基地局におけるマイクロセル伝搬損失推定", 電子情報通信学会論文誌B, Vol.J75-B2, No.8, pp.596-598
屋内環境
周波数
周波数 \(f \ [{\rm MHz}]\)\([{\rm MHz}]\)基地局端末間距離 \(d \ [{\rm m}]\)\([{\rm m}]\)1以上の値を入力-
基地局端末間床数 \(n\)123
-
基地局端末間床数 \(n\)
-
基地局端末間床数 \(n\)1
-
送信電力 \(P_{\rm t} \ [{\rm W}]\)\([{\rm W}]\)数値を入力してください送信アンテナ利得 \(G_{\rm t} \ [{\rm dBi}]\)\([{\rm dBi}]\)数値を入力してください
-
受信アンテナ利得 \(G_{\rm r} \ [{\rm dBi}]\)\([{\rm dBi}]\)数値を入力してください
-
伝搬損失\(L_{\rm total}\)= XXX.XX \([{\rm dB}]\)
-
電界強度
-
受信電力
- 計算式 - 伝搬損失(屋内環境)
-
減衰定数 \begin{align*} L_{\rm total} = 20 {\rm log}f + N {\rm log}d + L_{f}(n) - 28 \\ \end{align*} -
パラメータ \(\ f \ \) 周波数 \([{\rm MHz}]\) \(\ N \ \) 伝搬損モデルパラメータ \(\ d \ \) 基地局端末間の距離 \([{\rm m}]\) \(\ L_{f} \ \) 床の透過損 \([{\rm dB}]\) \(\ n \ \) 基地局端末間の床数 - 伝搬損モデルパラメータ \(N\)
-
周波数 住宅 オフィス 商業施設 900MHz - 33 20 1.2~1.3GHz - 32 22 1.8~2.0GHz 28 30 22 4GHz - 28 22 5.2GHz - 31 - 60GHz - 22 17
* 値が与えられていない場合は、オフィスのパラメータを準用する
- 伝搬損推定モデルパラメータ \(L_{f}\)
-
周波数 住宅 オフィス 商業施設 900MHz - 9(1階) - 19(2階) 24(3階) 1.8~2.0GHz 4\(n\) 15+4(\(n\)-1) 6+3(\(n\)-1) 5.2GHz - 16(1階) -
* 値が与えられていない場合は、オフィスのパラメータを準用する
- 参考文献
- [1] 細矢良雄監修, "電波伝搬ハンドブック", リアライズ理工センター出版
- [2] ITU-R Recommendation P.1238-2 "Propagation data and prediction methods for the planning of indoor radio communication systems and radio local area networks in the frequency range 900MHz to 100GHz", 2001.
トンネルの形状
円形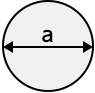 楕円形
楕円形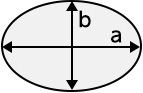 方形
方形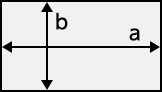 かまぼこ型
かまぼこ型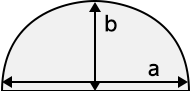 周波数 \(f \ [{\rm MHz}]\)\([{\rm MHz}]\)比誘電率 \(\varepsilon_{\rm r} \ (>1) \)1より大きい値を入力長径方向の長さ \(a \ [{\rm m}]\)\([{\rm m}]\)0より大きい値を入力短径方向の長さ \(b \ [{\rm m}]\)\([{\rm m}]\)\(b \leq a\) の値を入力距離 \(d \ [{\rm m}]\)\([{\rm m}]\)0より大きい値を入力✕ 条件:波長 \(\lambda \ \) = XXX.XXX \([{\rm m}] \) \(\leq \) 遮断波長 \(\lambda_{\rm c}\) = XXX.XXX \([{\rm m}]\) \(\left(= 2a \right) \)伝搬損失水平偏波 \(L_{\rm h}\)= XXX.XXX \([{\rm dB}]\)垂直偏波 \(L_{\rm v}\)= XXX.XXX \([{\rm dB}]\)減衰定数水平偏波 \(\alpha_{\rm h}\)= XXX.XXX \([{\rm dB/m}]\)垂直偏波 \(\alpha_{\rm v}\)= XXX.XXX \([{\rm dB/m}]\)
周波数 \(f \ [{\rm MHz}]\)\([{\rm MHz}]\)比誘電率 \(\varepsilon_{\rm r} \ (>1) \)1より大きい値を入力長径方向の長さ \(a \ [{\rm m}]\)\([{\rm m}]\)0より大きい値を入力短径方向の長さ \(b \ [{\rm m}]\)\([{\rm m}]\)\(b \leq a\) の値を入力距離 \(d \ [{\rm m}]\)\([{\rm m}]\)0より大きい値を入力✕ 条件:波長 \(\lambda \ \) = XXX.XXX \([{\rm m}] \) \(\leq \) 遮断波長 \(\lambda_{\rm c}\) = XXX.XXX \([{\rm m}]\) \(\left(= 2a \right) \)伝搬損失水平偏波 \(L_{\rm h}\)= XXX.XXX \([{\rm dB}]\)垂直偏波 \(L_{\rm v}\)= XXX.XXX \([{\rm dB}]\)減衰定数水平偏波 \(\alpha_{\rm h}\)= XXX.XXX \([{\rm dB/m}]\)垂直偏波 \(\alpha_{\rm v}\)= XXX.XXX \([{\rm dB/m}]\)- 計算式 - 減衰定数(トンネル)
-
減衰定数 水平偏波の減衰定数 \([{\rm dB/m}]\): \begin{align*} \alpha_{\rm h} = K_{\rm h} \lambda^{2} \left(\frac{\varepsilon_{\rm r}}{a^{3}\sqrt{\varepsilon_{\rm r}-1}} + \frac{1}{b^{3}\sqrt{\varepsilon_{\rm r}-1}} \right) \\ \end{align*} 垂直偏波の減衰定数 \([{\rm dB/m}]\): \begin{align*} \alpha_{\rm v} = K_{\rm v} \lambda^{2} \left(\frac{1}{a^{3}\sqrt{\varepsilon_{\rm r}-1}} + \frac{\varepsilon_{\rm r}}{b^{3}\sqrt{\varepsilon_{\rm r}-1}} \right) \\ \end{align*} -
パラメータ \(\ \alpha_{\rm v}, \ \alpha_{\rm h} \ \) 減衰定数 [垂直方向、水平方向] \([{\rm dB/m}]\) \(\ K_{\rm v}, \ K_{\rm h} \ \) 断面形状係数 [垂直方向、水平方向] \(\ \lambda \ \) 波長 \([{\rm m}]\) \(\ \varepsilon_{\rm r} \ \) 比誘電率 \(\ a \ \) 長径方向の長さ \([{\rm m}]\) \(\ b \ \) 短径方向の長さ \([{\rm m}]\) - 断面形状定数 \(K_{\rm h}, K_{\rm v} \)
-
円形 楕円形 方形 かまぼこ型 \(K_{\rm h}\) 5.09 4.45 4.34 5.13 \(K_{\rm v}\) 5.09 4.40 4.34 5.09 - 比誘電率 \(\varepsilon_{\rm r} \) (参考文献 [2])
-
空気 コンクリート
(乾燥)コンクリート
(湿潤)アスファルト
コンクリート\(\varepsilon_{\rm r}\) 1 4\(\sim\)6 8\(\sim\)20 4\(\sim\)6 - 参考文献
- [1] 細矢良雄監修, "電波伝搬ハンドブック", リアライズ理工センター出版
- [2] エネルギア総合研究所 第29号(2012年vol.3), 設備紹介, 電磁波レーダ鉄筋探索機
-
-